A Few of My Favorite Sigmoids
Here I’ll be looking at the subject of sigmoid functions from a somewhat unusual perspective: their suitability as a component in a digital musical instrument. I’ll consider how they sound, as well as efficiency of computing them.
A gallery of sigmoids
Below we’ll look at tanh, erf, an algebraic function, and hard clipping. For each we’ll show an audio clip and a spectrogram of a decaying sine wave run through the function.
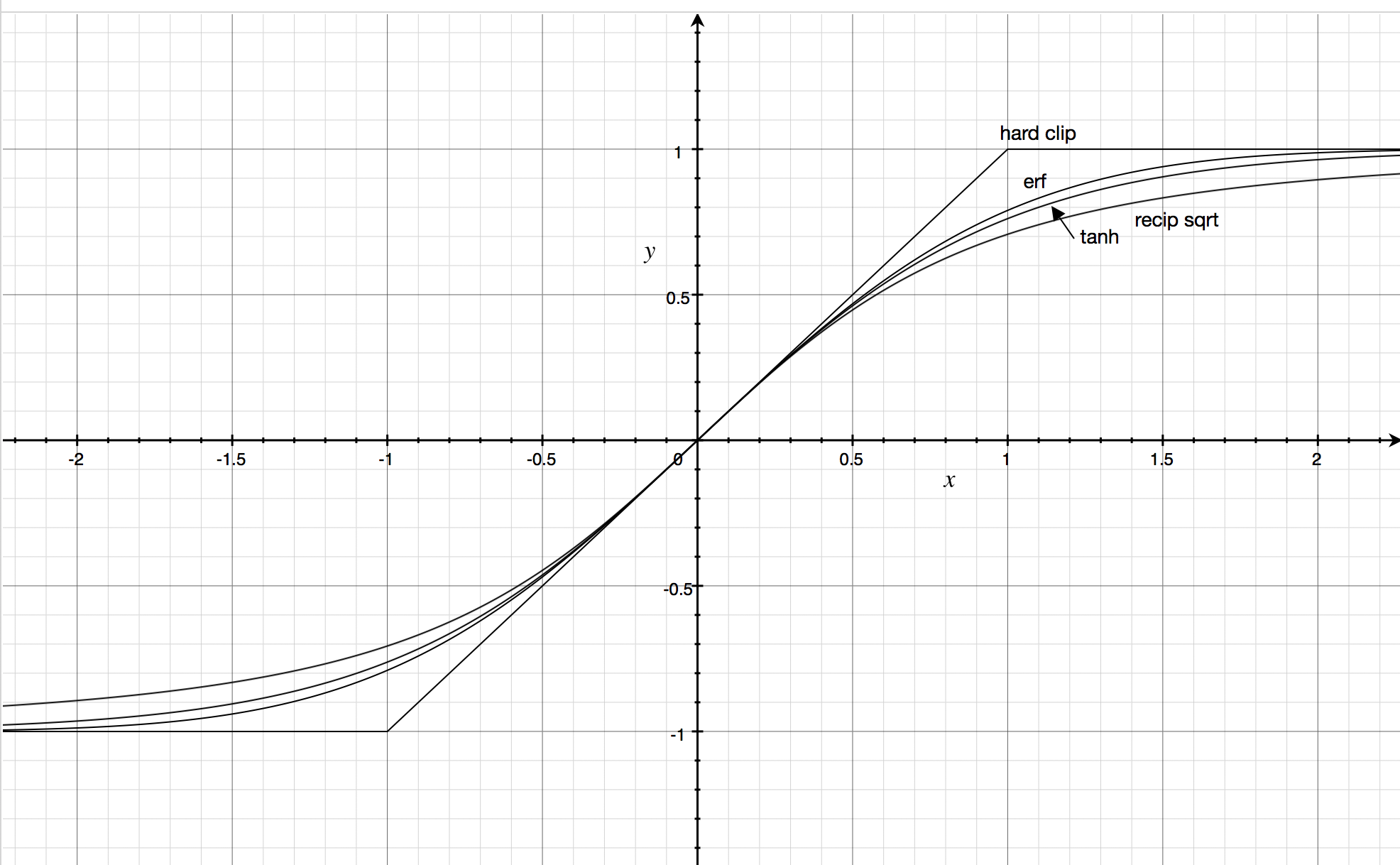
Hyperbolic tangent
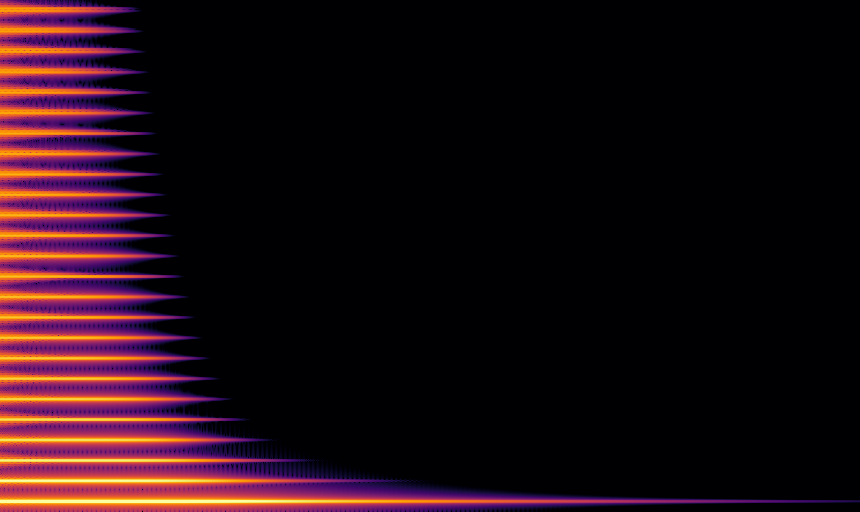
The hyperbolic tangent (or tanh) is arguably the most musical sigmoid function, so much so that the tanh3 Eurorack module provides the function implemented in analog electronics. As additional musical pedigree, it’s a good model of the response of differential transistor pairs as used in the Moog ladder filter.
The tanh can also be understood as a variant of the logistic function, with interpretation relating probability to Bayesian evidence. As such, it is often used as a nonlinear element in artificial neural networks (though ReLU) is gaining popularity).
Error function
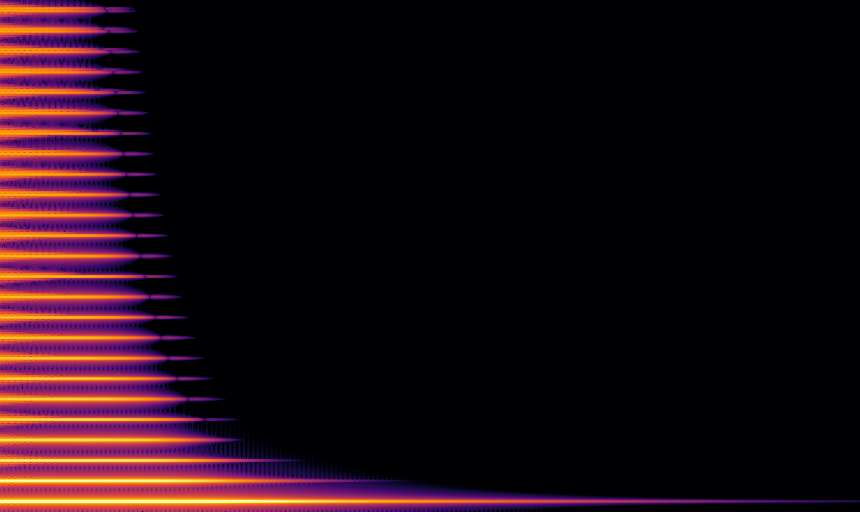
Another classic sigmoid is the “error function” (or erf). It’s sharper than tanh and approaches the asymptotes much more closely for large inputs.
One application of erf is efficient computation of the convolution of the Gaussian filter with a box, the 1D analog of a Gaussian blur applied to a rectangle. This can be used for accurate simulation of an oscilloscope, an important compotent in a serious electronic musician’s toolkit.
Reciprocal square root sigmoid
Another good sigmoid function is defined by this function:
\[\frac{x}{\sqrt{1 + x^2}}\]It’s fairly similar to tanh, but not quite as sharp, thus producing slightly more distortion at low-to-moderate input levels. One of the main reasons it’s interesting is that the central operation, an approximate reciprocal square root can be computed very efficiently. Fast reciprocal square root is the subject of an infamous snippet of code from John Carmack, and today the same basic technique powers very efficient SIMD implementations.
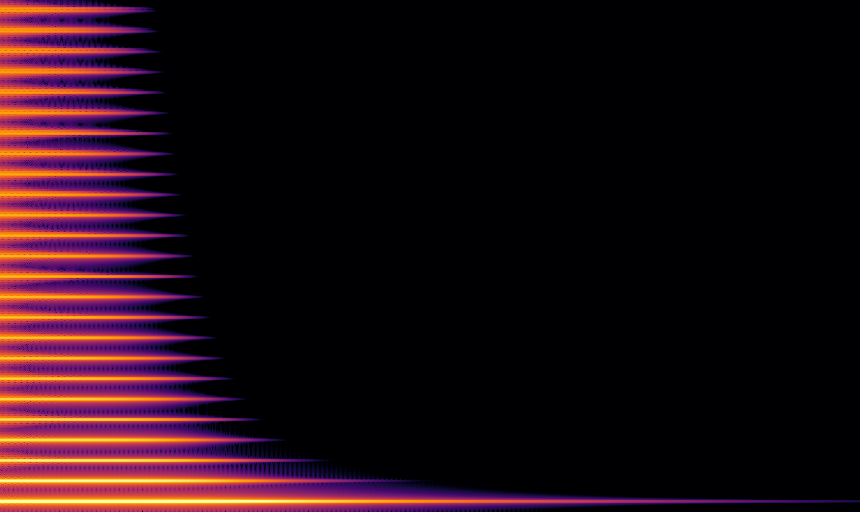
Hard clipping
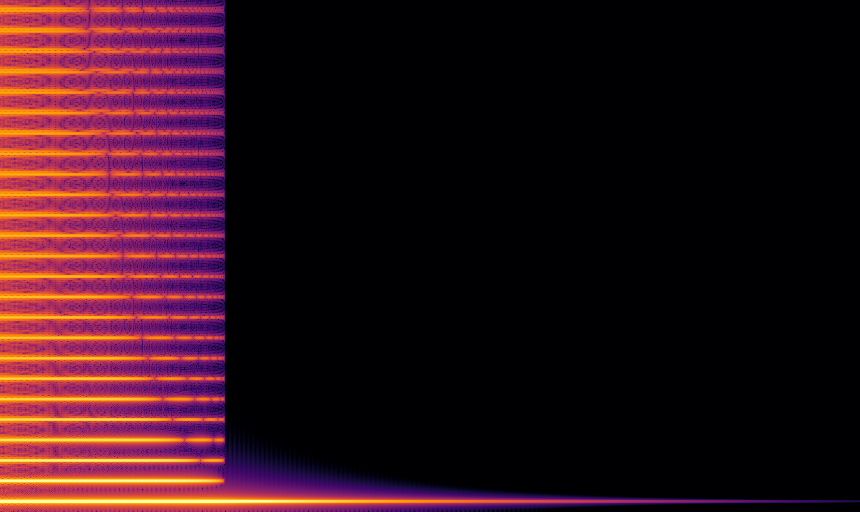
Hard clipping may not technically be a sigmoid function because of lack of smoothness, but is certainly important in audio contexts, so should be included, at least for comparison. It is the theoretical model of the distortion unit in pedals such as the RAT, but of course an analog pedal isn’t subject to aliasing, and it’s likely that the imperfections from producing a pure hard-clip transfer function actually smooth the sound.
Aesthetic comparison
To my ears, tanh sounds the best. It has more interesting harmonics at high drive amplitudes (and just sounds louder), and smoother at low. This is of course incredibly subjective, and I’m probably biased.
Looking at the spectra, there are other reasons to prefer tanh. For digital audio, you want distortion that produces harmonics up to some point and then falls off quickly, because any harmonics above the Nyquist frequency turn into aliasing. Of course, it’s also possible to mitigate aliasing by running the chain at a higher frequency, but that increases computational load. For reasons that are still somewhat mysterious to me, the spectra of tanh seems to fall off more rapidly, even though it’s a sharper knee than the recip-sqrt one.
The spectrum of erf has odd nulls in it that are not present in either tanh or
Hard clipping doesn’t sound good at all. The distortion sounds harsh, and the higher harmonics produce aliasing.
Fast implementations
Rust language benchmarks for the implementations are here; timings are based on runs of that code on a i7-7700HQ @2.8GHz.
Looking at the straightforward implementations of the tanh and recip-sqrt sigmoids, we see a huge difference: 5.9 vs .453 nanoseconds, respectively, a 13x difference. What’s going on? There are basically two things. First, for a simple algebraic formula (including sqrt), Rust is able to optimize the scalar function into vector code, while the tanh is a function call that must be evaluated sequentially. Second, the recip-sqrt is just a lot fewer operations, all of which are implemented efficiently.
On the hardware I’m testing on, writing explicit SIMD code is only a small speedup (to 0.4ns). I think this is because the sqrt instruction is already implemented very efficiently. On ARM, it would likely be a different story, as ARM has an instructions for approximate reciprocal square root (vrsqrte and vrsqrts) but not a full, accurate square root.
Morphing with polynomials
My favorite way to reasonably accurately approximate other sigmoids (including tanh and erf) is to pre-process the input through a low-order, odd polynomial. This technique is both faster and more accurate than published approximations. In addition, its errors are smooth (unlike piecewise approximations), so they sound almost identical to the precise functions; the spectrum is basically the same, only tiny differences in the amplitudes of the spectral peaks of the harmonics.
For tanh, this polynomial should approximate sinh, based on the identity:
\[\tanh x = \frac{\sinh x}{\sqrt{1 + (\sinh x)^2}}\]The polynomial doesn’t have to be very accurate though, especially at larger values, as they get squished out by the subsequent sigmoid. A good compromise is a fifth-order odd polynomial, yielding an accuracy of 2e-4 at 0.55ns per sample.
For comparison are two other approximations from the literature. For tanh, the Deep Voice neural net paper includes a rational polynomial based on an approximation to $e^x$. In my testing, it has an accuracy of around 1.5e-3 at 0.7ns.
For erf, one of the most common approximations is due to Abramowitz and Stegun (it’s the source for the oscilloscope code). It has an accuracy of 5e-4, and take 0.86ns per sample, which is quite good, as it’s a rational polynomial at heart. But morphing beats it. Using a 7th order polynomial to surpass the accuracy (2.2e-4) is still faster: 0.63ns.
Conclusion
I’ve presented an argument that tanh is the best sigmoid function for digital music applications, though others are usable, and a function based on reciprocal square root behaves similarly and is faster. I’ve also presented implementations of tanh and erf sigmoid functions which are reasonably accurate numerically, high quality for audio applications, and faster than other commonly used implementations.